有了一元线性回归试验(day_2)基础之后, 我们得以尝试较为复杂多元线性回归试验。在day_3中，我们将根据给定的数据集50_Startups.csv，通过其中的自变量 R&D Spend、 Administration、Marketing Spend 、 State字段预测因变量Profits的。

 

本文将涵盖以下内容：

  1.          day_3源码学习及逐步分析；
  2.          为何及如何避免Dummy Variable Trap；
  3.          one-hot及其他常用的编码方式 ；
  4.          多元线性回归的相关知识补充;
  5.          使用excel完成day_3的回归分析任务；

 

day_3内容学习及逐步分析

数据集
数据集

此部分内容与【Flag】机器学习100天-[第2天]-线性回归 中代码的部分别无二致，因此，如非必要，将仅做简略的步骤说明。

首先，我们通过下方命令，将读取数据集并将其拆分成训练集以及测试集。并查看拆分后的结果。

1
2
3
4
5
6
7
8
9
10
import pandas as pd
import numpy as np

 

dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[ : , :-1].values
Y = dataset.iloc[ : , 4 ].values
# print("X:",X, "\n")
# print("Y:",Y, "\n")

解析分类数据，并对第四列进行onehot编码

1
2
3
4
5
6
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder = LabelEncoder()
X[: , 3] = labelencoder.fit_transform(X[ : , 3])
onehotencoder = OneHotEncoder(categorical_features = [3])
X = onehotencoder.fit_transform(X).toarray()
print(X)

 

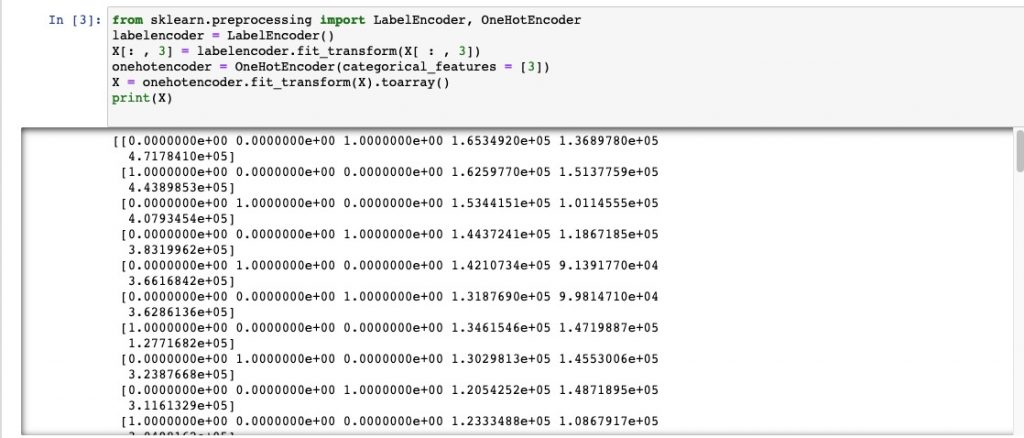
Avoid Dummy Variable Trap：本文中与前篇中代码最大的不同就在于此。通过 X = X[: , 1:] 将经过one-hot encode的 state变量 截去首位来避免虚拟变量陷阱。在本文接下来的 为何及如何避免Dummy Variable Trap 部分，我们将尝试阐述虚拟变量产生的原因及如何避免虚拟变量陷阱。

1
2
X = X[: , 1:]
print(X)

拆分训练集以及测试集。并查看拆分后的结果。

1
2
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2, random_state = 0)

 

使用训练集X_train, Y_train 进行线性回归

1
2
3
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, Y_train)

 

使用测试集Y_test, X_test 数据检验回归方程regressor

1
2
3
y_pred = regressor.predict(X_test)
print(y_pred)
print(Y_test)
测试集数据验证
测试集数据验证

 

 

 为何及如何避免Dummy Variable Trap(虚拟变量陷阱)

产生原因

当我们将一个变量进行one-hot编码之后，会产生多个虚拟变量。而当产生的虚拟变量之间存在线性关系时(multi-colinear)，即可以通过一个变量可以预测到另一个变量。multi-colinear会让我们对回归系数(coefficient)计算结果变得不稳定。

我们用图形来解释。

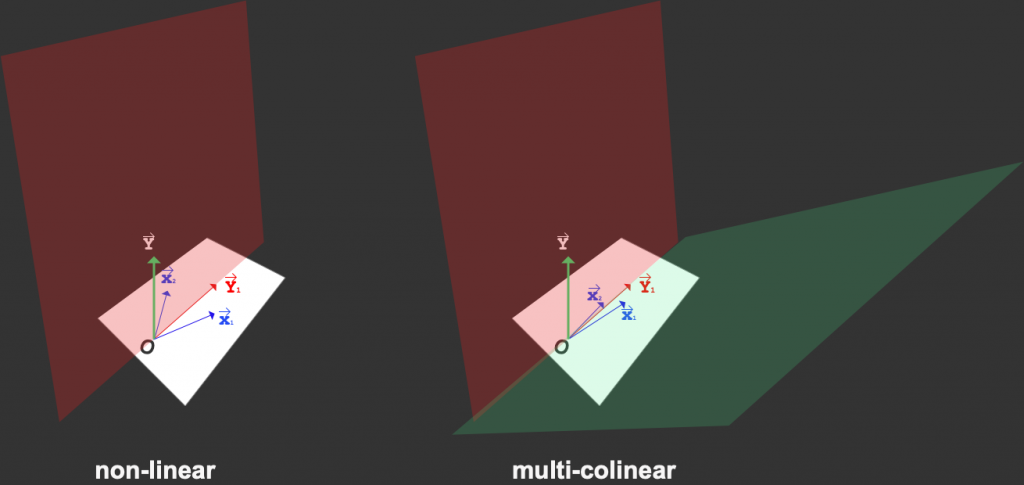
multi-colinear的图形解释
multi-colinear的图形解释(Axure绘制)

 

我们假设只有两个自变量向量(独热编码后的变量) X1、 X2。 Y为因变量，那么 Y1 即为Predictions。 当X1、 X2无线性关系时，则两个向量之间存在夹角，可确定唯一的一个投影，进而可确定唯一平面(non-linear - 红色);而当 X1、 X2 存在线性关系时，由于向量共线。因而无法确定一个平面(multi-colinear - 红色/绿色) ，这将导致 Y1 不确定，即coefficient β不稳定。

 

 

如果从代数方面看，基于最小二乘法，coefficient β可以视为下述公式计算

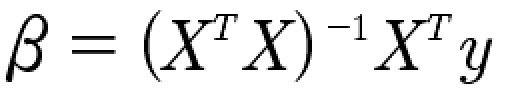
可以看作自变量的协方差矩阵。如果有两个自变量存在完全线性关系，协方差矩阵中就会有两列变量向量表现线性关系(可互相预测)，这将导致协方差矩阵不可逆(无逆矩阵)。而在上述公式中，存在求逆矩阵的计算过程()，两者互相矛盾，所以我们无法找到解  β。

 

注意：

  1. 矩阵乘法、矩阵的逆、以及transpose的计算方法可参考 线性代数基础。
  2. 代码解释可参考Dummy Variable Trap
  3. A矩阵不可逆
    <=> |A| = 0
    <=> A的列(行)向量组线性相关
    <=> R(A)<n
    <=> AX=0 有非零解
    <=> A有特征值0.
    <=> A不能表示成初等矩阵的乘积
    <=> A的等价标准形不是单位矩阵

 

处理方式

如果一个变量经过one-hot encode得到的虚拟变量类别有  n  位，则可以仅使用  n-1  个虚拟变量，那么将经过one-hot encode的 state变量 截去首位，即可避免multi-colinearity。

 

One-hot及其他常用的编码方式

Day 3的实践，在使用one-hot encoding时，可以发现其存在的一些问题：

  1. 当需要编码的变量较多时，即容易大幅数据的维度，增加运算量；
  2. 容易产生因multi-colinearity导致的coefficient不稳定；
  3. 部分算法需要对变量数值敏感，此时不适用one-hot encoding;

如果我们进行思考，我们大概率会提出问题：常用的编码方式有哪些？适用场景是哪些？每种编码方式适用的自变量类型？我们从day 1 至今 我们在学习内容中遇到过的部分编码方式进行解读。后续将持续更新。

 

One-hot Encoding

通常用于不具备大小、顺序的区分的 定类变量 的编码。其特点是是讲定类变量转换成由0 和 1 组成的向量。但缺点也显而易见，即上文所述的虚拟变量陷阱

如：

1
2
3
4
5
6
7
8
9
10
11
import pandas as pd
from sklearn.preprocessing import OneHotEncoder

categorical_df = pd.DataFrame({'my_id': ['101', '102', '103', '104'],
'name': ['allen', 'bob', 'chartten', 'dory'],
'place': ['third', 'second', 'first', 'second']})
print(categorical_df)
print('--'*20)

encoder = OneHotEncoder(categories=[['dory', 'bob', 'chartten', 'allen']])
encoder.fit_transform(categorical_df[['name']]).toarray()

我们自定义的编码顺序是['dory', 'bob', 'chartten', 'allen']，dory=[1,0,0,0], bob=[0,1,0,0], chartten=[0,0,1,0], allen=[0,0,0,1],  在输出结果的第一列中表示allen，即为[0,0,0,1]，第二列表示bob，即为[0,1,0,0]，以此类推。

 

Label Encoding

Label Encoding是给某一列数据编码，通常用于 定续变量 的编码。

值得注意的是，定序变量 和 定类变量一样，也是分类，但有排序逻辑关系，等级上高于定类。比如，学历分小学，初中，高中，本科，研究生，各个类别之间存在一定的逻辑，显然研究生学历是最高的，小学最低。这时候使用Label encoding会显得更合适，因为自定义的数字顺序可以不破坏原有逻辑，并与这个逻辑相对应。 但一个变量是 定类 还是 定续，这很大程度上取决于你自身对研究的理解，因此我们并不能规定哪些情况一定要将其解释为定续，哪些情况又要将其解释为定类。

 

另外，编码方式还会在一定程度上影响数据在“数值”上的剧烈程度。

如，我们对数据进行如下处理

1
2
3
4
5
6
7
8
9
10
11
12
13
import pandas as pd
from sklearn.preprocessing import LabelEncoder

categorical_df = pd.DataFrame({'my_id': ['101', '102', '103', '104'],
'name': ['allen', 'bob', 'chartten', 'dory'],
'place': ['third', 'second', 'first', 'second'],
})
print(categorical_df)
print('--' * 20)

encoder = LabelEncoder()
categorical_df['place']=encoder.fit_transform(categorical_df['place'])
print(categorical_df)

输出结果：

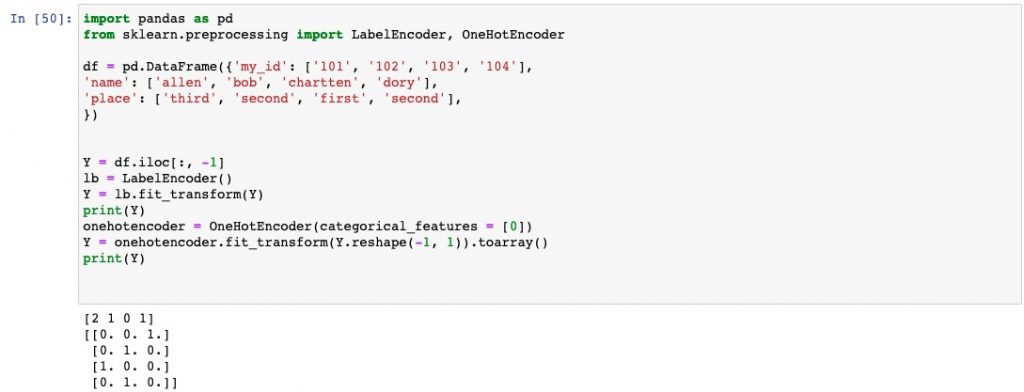
我们通过label encode 将place 编码成了 [0, 2]; 而one hot encode则将其编码成了 0 和 1 （注意到：我在图中先将其进行label encode 再 one hot encode是由于sklearn版本较低原因：该列是string而低版本sklearn 进行one hot encode的要求输入的2D array(-like)）

但不可思议的是，我们使用的版本确实是 0.20.0 (day_0:安装sklearn)。而且之前，也确实可以直接进行独热编码；百思不得其解。

 

 

使用注意事项：

所使用的模型对数值大小敏感的模型：必须使用one-hot encoding。典型的例子就是LR和SVM。二者的损失函数对数值大小是敏感的，并且变量间的数值大小是有比较意义的。而Label encoding的数字编码没有数值大小的含义，只是一种排序，因此对于这些模型都使用one-hot encoding。

对数值大小不敏感的模型（如树模型）：不建议使用one-hot encoding。一般这类模型为树模型。如果分类类别特别多，那么one-hot encoding会分裂出很多特征变量。这时候，如果我们限制了树模型的深度而不能向下分裂的话，一些特征变量可能就因为模型无法继续分裂而被舍弃损失掉了。因此，此种情况下可以考虑使用Label encoding

 

待后续更新

 

多元线性回归的相关知识补充

Pearson 系数

统计学的相关系数经常使用的有三种:皮尔森（pearson）相关系数和斯皮尔曼（spearman）相关系数和肯德尔（kendall）相关系数.皮尔森相关系数是衡量线性关联性的程度，p的一个几何解释是其代表两个变量的取值根据均值集中后构成的向量之间夹角的余弦.

相关系数：考察两个事物（在数据里我们称之为变量）之间的相关程度。

如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：

(1)、当相关系数为0时，X和Y两变量无关系。

(2)、当X的值增大（减小），Y值增大（减小），两个变量为正相关，相关系数在0.00与1.00之间。

(3)、当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在-1.00与0.00之间。

 

相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。

通常情况下通过以下取值范围判断变量的相关强度：
相关系数 0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关

皮尔森(pearson)相关系数
在这三大相关系数中，spearman和kendall属于等级相关系数亦称为“秩相关系数”，是反映等级相关程度的统计分析指标。今天暂时用不到，所以现在只做pearson的相关研究。

其计算公式为：

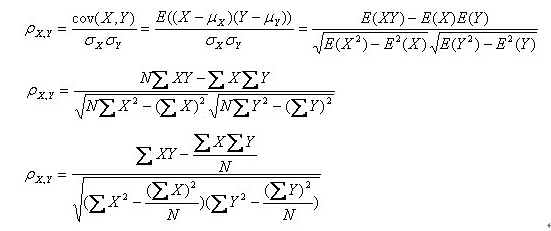
pearson coefficient
pearson coefficient

为方便计算，我们一般采用第二个公式。参考我大学课本。

回归系数

参考以下链接：

  1. What is a regression coefficient?
  2. 回归系数

 

使用excel完成day_3的回归分析任务

使用excel进行回归分析
使用excel进行回归分析

下载本次分析文件：

50_Startups" rel="external" target="_blank" title="下载地址"> Download

 

我们使用excel进行回归分析，查看各个变量对最终profits的影响：

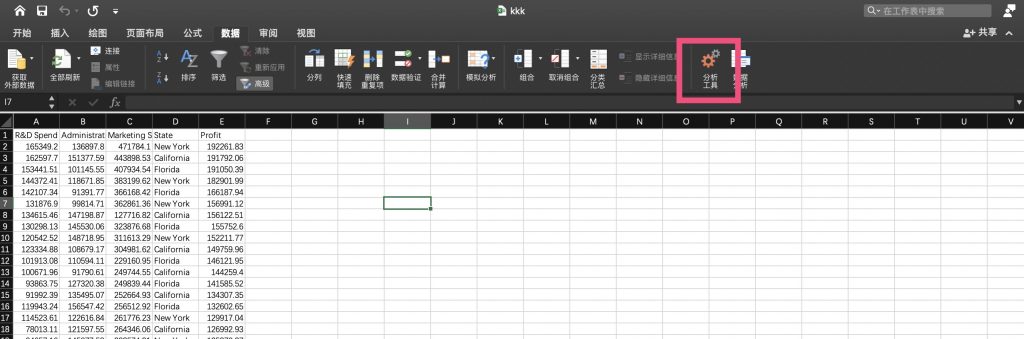
  • 打开数据集，并切换到数据工具栏：

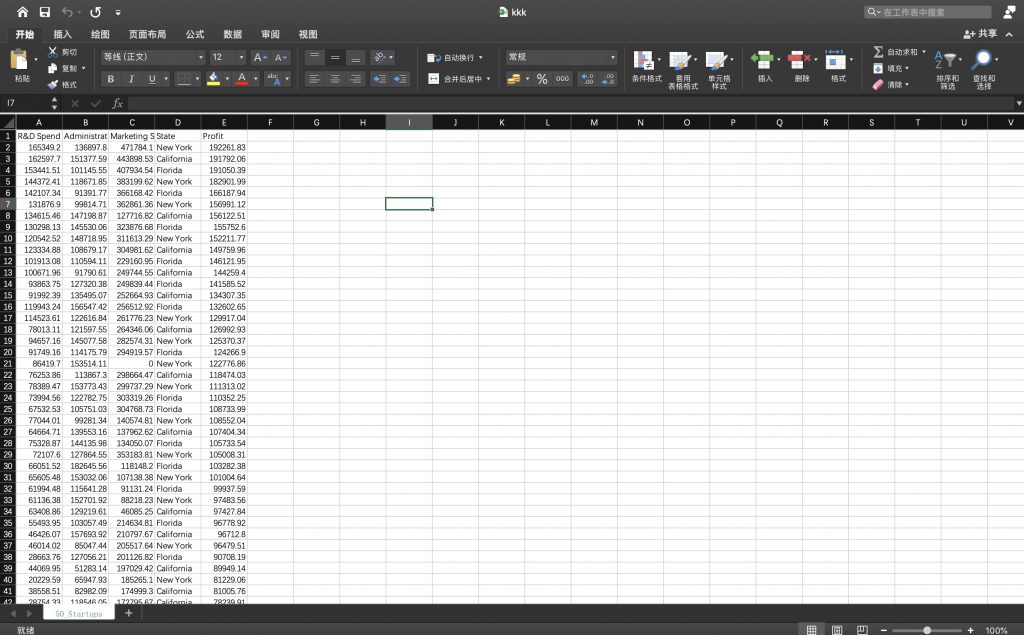
  •  点击分析工具 并 把分析工具库勾选上：

 

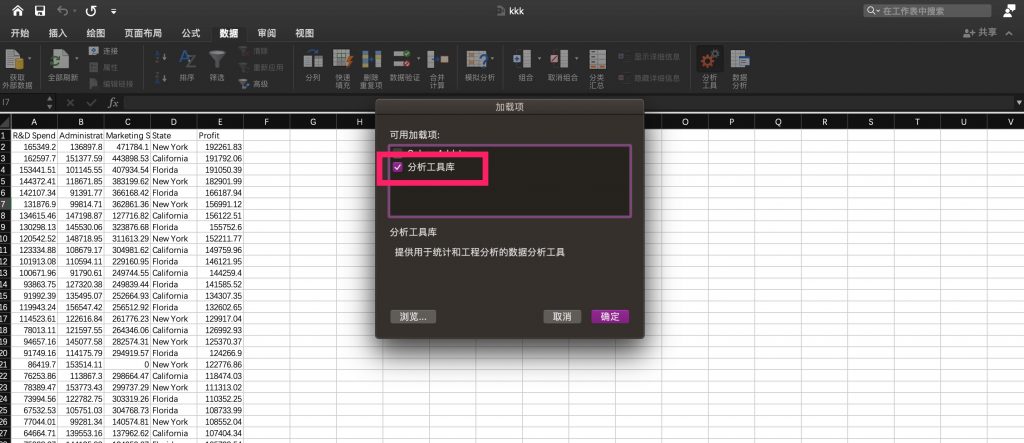
  • 然后再次回到工具栏点击点击数据分析后选择回归并确定，此外注意其中的state变量，我们已经将其替换为one hot变量；

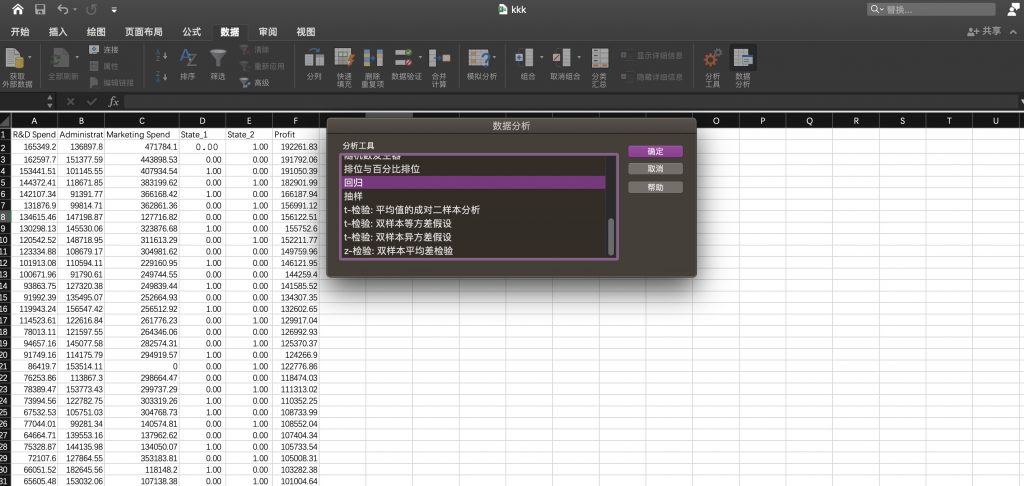
  • 选择对应的变量区域。注意由于我们是希望通过(R&D Spend， Administration，Marketing Spend ，State_1 ，State_2)来预测收益profit。因此我们需按照下图所示选择对应的自变量、因变量区域。

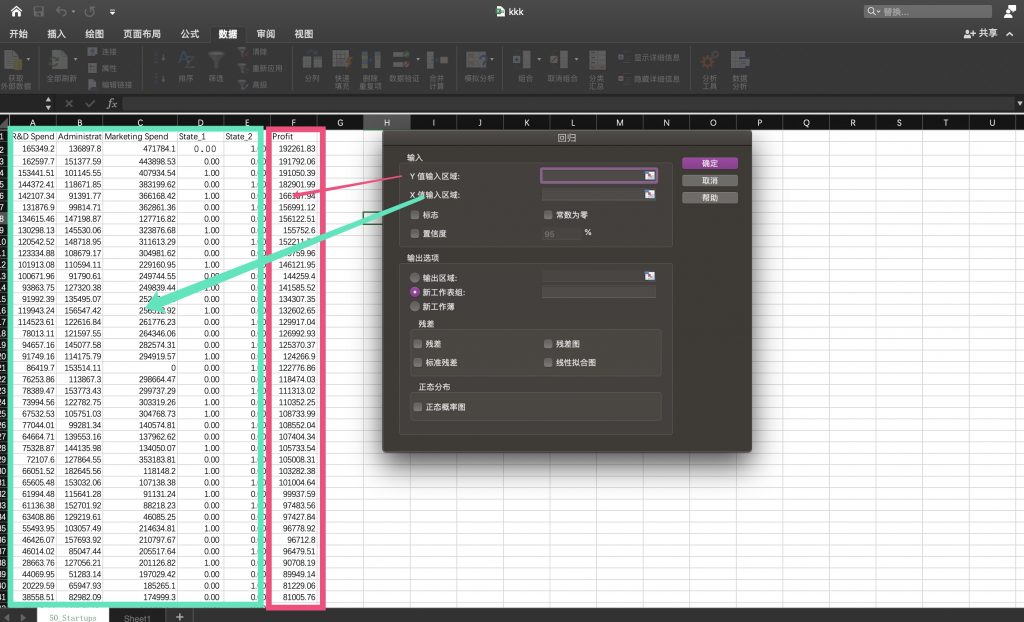
  • 最终数据输入如下

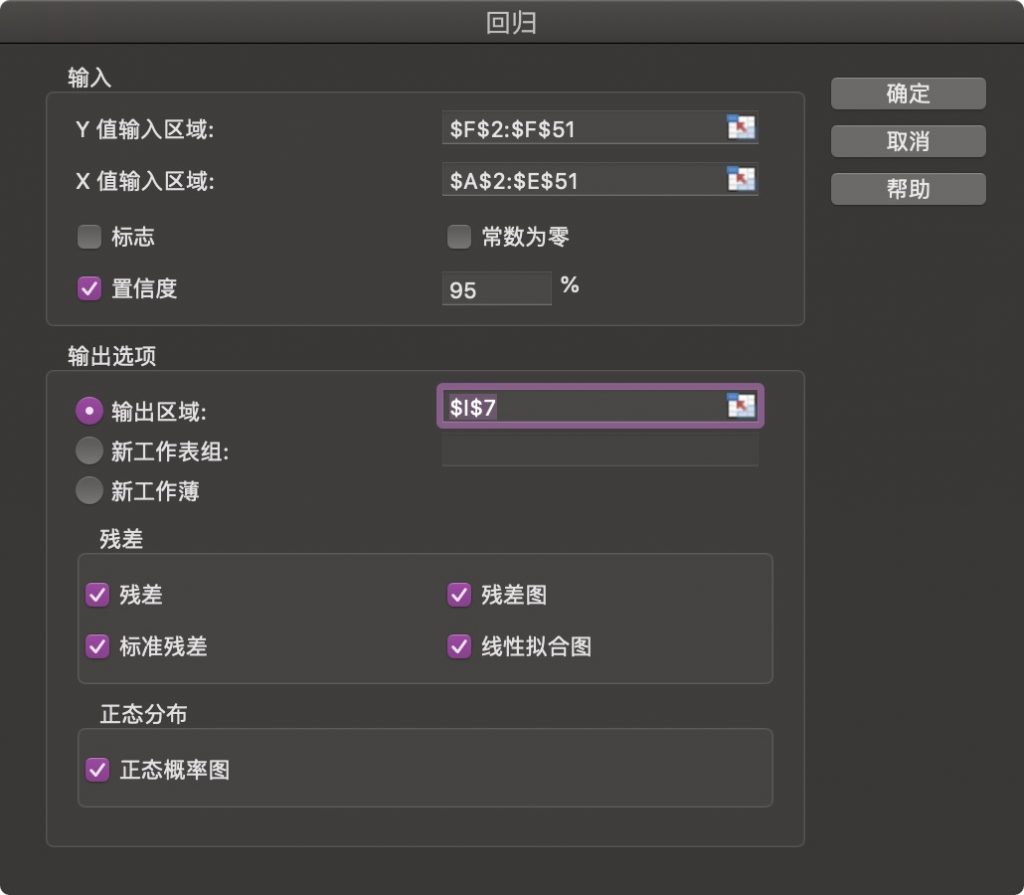
  • 最后点击确定，在稍作处理，我们即可得到分析结果

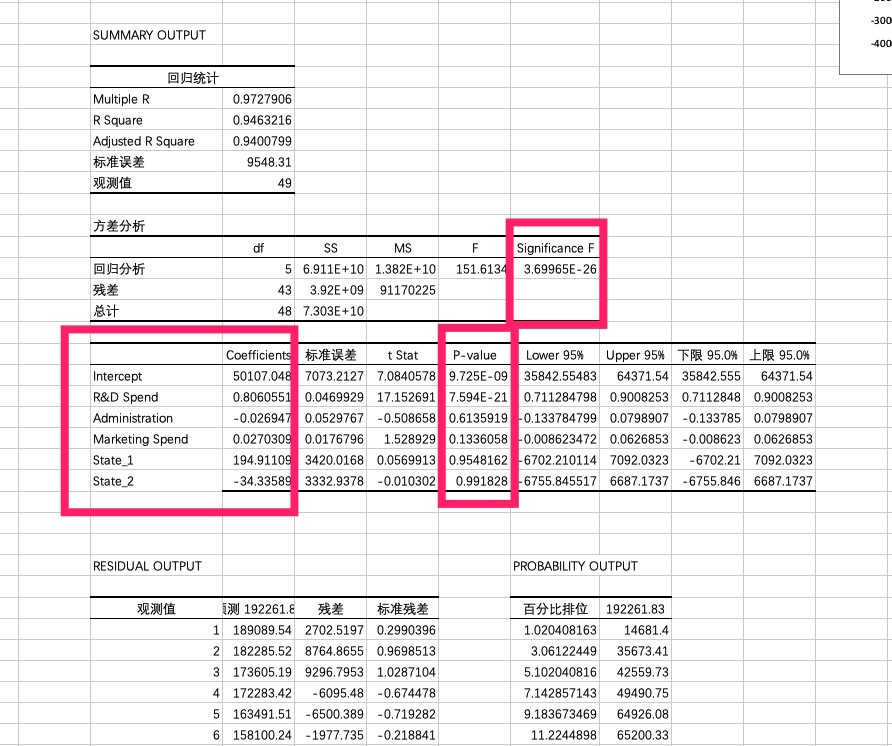
关键表格：

Coefficients 标准误差 t Stat P-value Lower 95% Upper 95% 下限 95.0% 上限 95.0%
Intercept 50107.0476 7073.21266 7.08405784 9.725E-09 35842.55483 64371.5404 35842.5548 64371.5404
R&D Spend 0.80605506 0.04699292 17.1526911 7.5942E-21 0.711284798 0.90082531 0.7112848 0.90082531
Administration -0.026947 0.05297673 -0.5086582 0.61359188 -0.133784799 0.07989071 -0.1337848 0.07989071
Marketing Spend 0.02703089 0.01767963 1.52892896 0.13360578 -0.008623472 0.06268526 -0.0086235 0.06268526
State_1 194.911089 3420.0168 0.05699127 0.95481616 -6702.210114 7092.03229 -6702.2101 7092.03229
State_2 -34.335888 3332.93778 -0.010302 0.991828 -6755.845517 6687.17374 -6755.8455 6687.17374

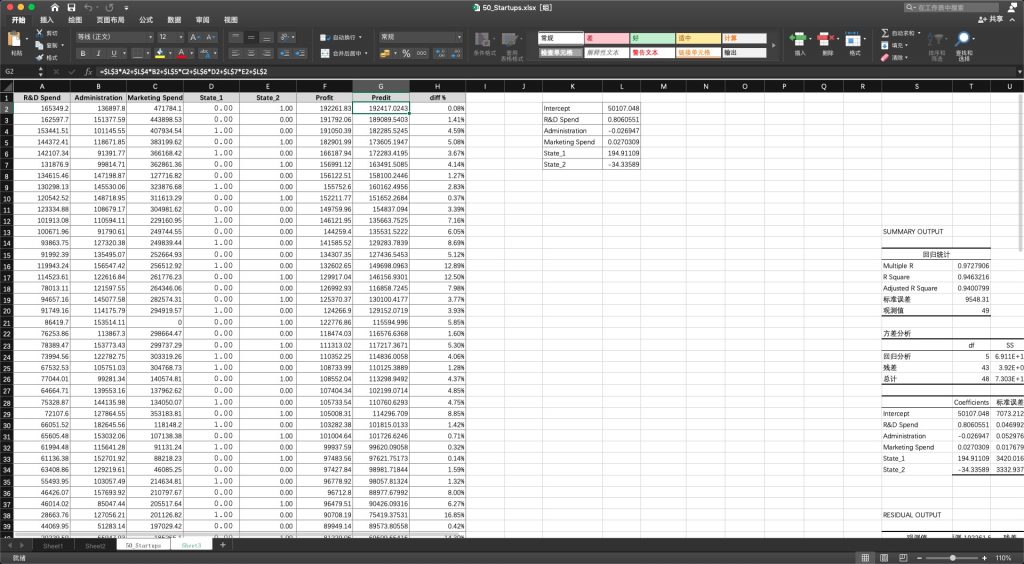
通过表格中红色和绿色部分的数据，即coefficient以及对应变量的p-value；我们其实可以发，在自变量中，仅 R&D Spend 与 收益profits是存在极强的线性关系，其他部分(忽略截距)与profit之间的关系其实并不显著。

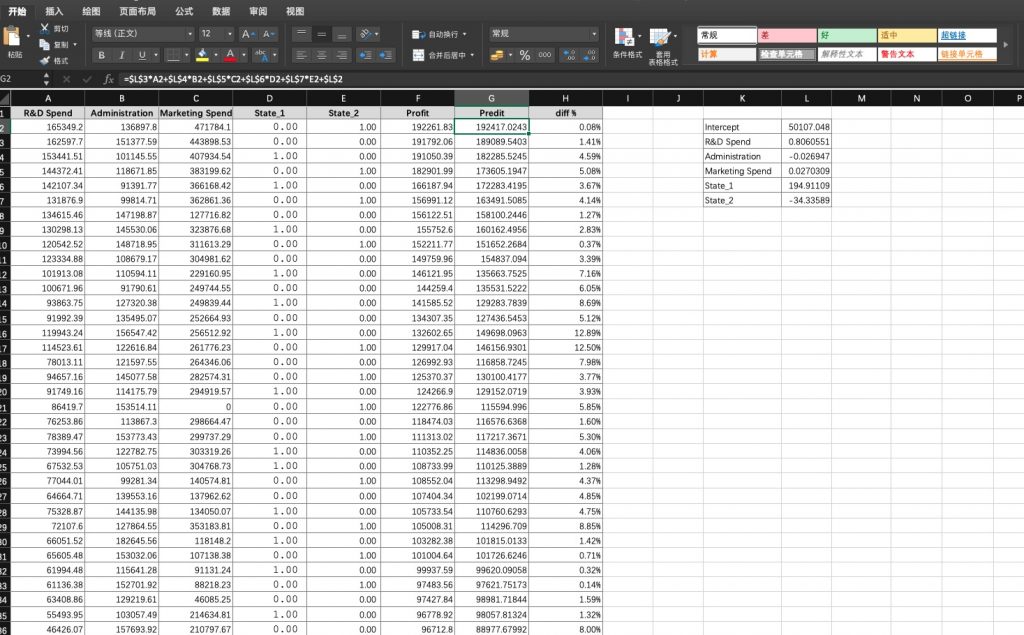
其他：

1、再看回归统计表，Multiple R即相关系数R的值，和我们之前做相关分析得到的值一样，大于0.8表示强正相关。

2、回归统计表中的R Square是R平方值，R平方即R的平方，又可以叫判定系数、拟合优度，取值范围是[0,1],R平方值越大，表示模型拟合的越好。一般大于70%就算拟合的不错，60%以下的就需要修正模型了。这个案例里R平方0.9054，相当不错。

3、Adjusted R是调整后的R方，这个值是用来修正因自变量个数增加而导致模型拟合效果过高的情况，多用于衡量多重线性回归。

4、第二张表，方差分析表，df是自由度，SS是平方和，MS是均方，F是F统计量，Significance F是回归方程总体的显著性检验，其中我们主要关注F检验的结果，即Significance F值，F检验主要是检验因变量与自变量之间的线性关系是否显著，用线性模型来描述他们之间的关系是否恰当，越小越显著。这个案例里F值很小，说明因变量与自变量之间显著。

5、残差是实际值与预测值之间的差，残差图用于回归诊断，回归模型在理想条件下的残差图是服从正态分布的。

6、第三张表我们重点关注P-value，也就是P值，用来检验回归方程系数的显著性，又叫T检验，T检验看P值，是在显著性水平α（常用取值0.01或0.05）下F的临界值，一般以此来衡量检验结果是否具有显著性，如果P值>0.05，则结果不具有显著的统计学意义，如果0.01<p值<0.05，则结果具有显著的统计学意义，如果p<=0.01，则结果具有极其显著的统计学意义。t检验是看某一个自变量对于因变量的线性显著性，如果该自变量不显著，则可以从模型中剔除。< p=""></p值<0.05，则结果具有显著的统计学意义，如果p<=0.01，则结果具有极其显著的统计学意义。t检验是看某一个自变量对于因变量的线性显著性，如果该自变量不显著，则可以从模型中剔除。<>

7、从第三张表的第一列我们可以得到这个回归模型的方程：

y=0.806055055153988R&D Spend-0.0269470461000727Administration+0.0270308927158894Marketing Spend+194.911088853033State_1-34.3358883075974State_2+50107.0476300378

 

此后对于每一个输入的自变量x,都可以根据这个回归方程来预测出因变量Y。

 

笔记下载

day_3" rel="external" target="_blank" title="下载地址"> Download