在本篇内容中,我们将会进行简单线性回归的实现,尝试通过数据集studentscores中学生的学习小时数 Hours 来预测学生的考试得分 Scores .
本篇内容的笔记项目结构如下图所示。准备就绪,前一天内容请查阅这里
导入数据集并切分训练集和测试集
本次的测试集大小为数据集的25%, 重复代码的解释可在 day_1 中查看,这里就不再赘述
打开 studentscores.csv。我们可以看到,这是 25 × 2 的数据。 知晓了数据的基本结构之后,我们接下来将通过 sklearn 来对这些数据进行线性回归的拟合操作。

首先,我们通过下方命令,将读取数据集并将其拆分成训练集以及测试集。并查看拆分后的结果。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
dataset = pd.read_csv('studentscores.csv')
X = dataset.iloc[ : , : 1 ].values
Y = dataset.iloc[ : , 1 ].values
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split( X, Y, test_size = 1/4, random_state = 0)
print("X_train:", X_train)
print("X_test:", X_test)
print("Y_train:", Y_train)
print("Y_test:", Y_test)
导入数据运行结果如下图所示:

使用训练集X_train, Y_train 进行线性回归
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor = regressor.fit(X_train, Y_train)
print(regressor.coef_)
输出结果回归系数coefficient:[9.94167834]
其中 regressor.fit(X_train, Y_train) 方法则是在对X_train, Y_train 进行线性拟合。 注意,sklearn 在此处进行拟合时采用的是 最小二乘法, 而非 梯度下降法 。
数据可视化
使用训练集X_train, Y_train 数据查看回归方程拟合效果
使用matplotlib绘制散点图及函数图像,进行测试集数据可视化
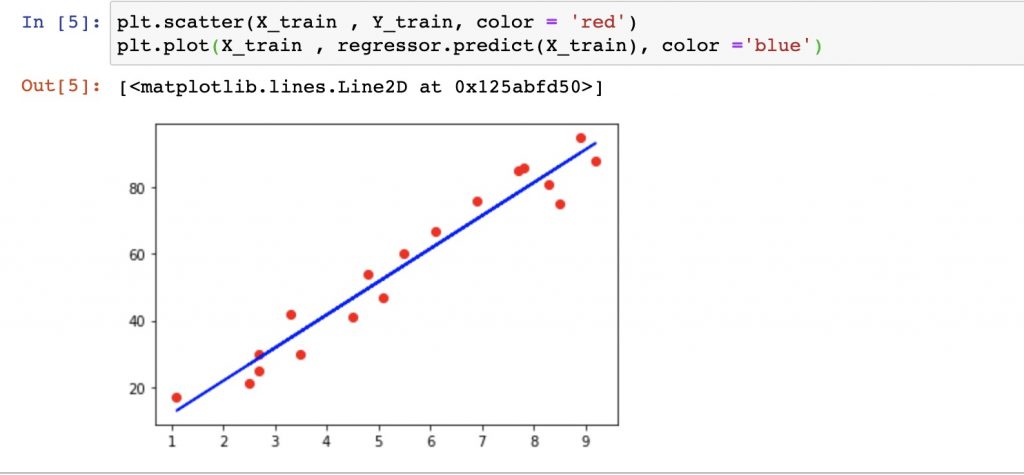
plt.scatter(X_train , Y_train, color = 'red')
plt.plot(X_train , regressor.predict(X_train), color ='blue')
使用测试集Y_test, X_test 数据检验回归方程regressor
Y_pred = regressor.predict(X_test)
print(Y_pred)
精确值:

regressor计算值:
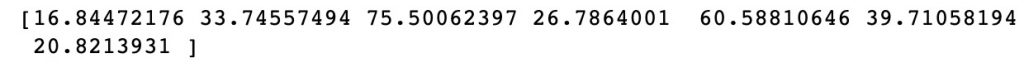
使用matplotlib绘制散点图及函数图像,进行测试集数据可视化:
plt.scatter(X_test , Y_test, color = 'red')
# plt.plot(X_test , regressor.predict(X_test), color ='blue')
print("==="*5)
plt.plot(X_test , Y_pred, color ='blue')

补充内容
线性回归原理
在本文中,当我们谈到线性回归时,我们实际上在说的是一元线性回归。就是当我们知道事物的一个性质时,可以知道另一个确定的性质。即:一般来说我们会通过一个定距变量去预测另一个定距变量,如下方的例子。
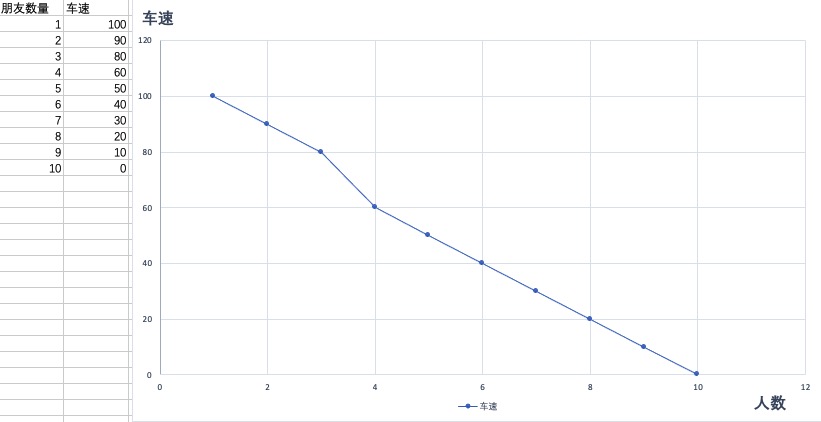
例如:我们知道小明有一辆三轮自行车,他会踩自行车载他朋友。当他载1个朋友时 ,踩的速度能达到100km/h,;载两个朋友时,踩的速度只能到90km/h......
但有时有我们也可以通过对一个定距变量的观察,去预测一个定类变量的结果,如通过平均体重去预测成年男女性别
所以,如果你足够敏锐,就可以发现,在某些合适的情况下,我们可以通过设置合适的数量阈值,从而将分类问题转化为线性回归问题。例如的成年男女性别预测的例子,我们可以定义平均体重在区间 [50KG, 60KG) 之间的定义为成年女性,在区间 [60KG, 90KG) 范围内的定义为成年男性。 但实际上,这种分类问题,一般使用逻辑回归。
一元线性回归
我们知道二元一次方程。我们一般设置y为因变量,x为自变量。对于给定的α ,β;

上方的公式在直角坐标系中,是一条特定的直线,这就是为什么我们会将其成为【线性】回归的原因。
而在上方公式中,因为我们是用一个自变量变量 x 来预测应变量 y。也就是说,我们在扔了一条直线在一堆数据点中,并不断上下移动(调整β)、旋转(调整α)这条直线来拟合数据。
如在今天的数据集中,我们将学生学习小时数和最终考试结果分数的数据点在坐标中标注出来。其中,横坐标为学习小时数,纵坐标为考试分数。

我们观察上图,红点部分表示的是“不准确”的现实世界中的数据,而蓝线则是我们期望找到的“准确关系”(这里我偷懒了,直接用了计算出来的函数),即,我们输如一个学习小时数,能够返回一个准确且唯一的分数。但我们不难发现,每个确定的现实红点与“关系”之间似乎总是不能完美地“贴合”,也就是说,我们用存在的某个“准确关系”计算出来的值(蓝线上的值)与实际红点的值总会“不可避免”地存在差值,即 误差。那么我们可在原有的线性方程中添加一个参数 ε 来描述这种差距:

损失厌恶和损失函数
基本逻辑
此时,我们修改意思下公式,注意下标 i :
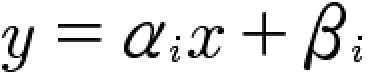
之前我们提到,显示数据与拟合曲线之间总是存在误差。那么我们就希望我们拟合出来的曲线是与真实数据之间的误差 ε 最小的。因此,我们尝试不断调整α 和 β。来让曲线拟合的值与真实数据值之间的误差尽可能小。同时,我们也很容易发现,无论我们对 α 和 β怎么调整,由于一元一次函数是直线。也就意为这对某个点的误差变小的时候,对另外的点的误差则可能增大。因此,我们转而总览全局,不要求我们的函数对某个数据点的误差最小,【但要求它与所有的数据点的误差的和最小。】
即:
此处,我们约定![]() 为真实值,
为真实值, ![]() 为预测值。即,我们用每一个点的真实值减去预测值,得到一个点的误差,在将所有数据点的误差累加,即可算出误差的和。但,这样做的可能存在正负值互相抵消的情况。因此,我们调整下公式并进行推导, 得到损失函数:
为预测值。即,我们用每一个点的真实值减去预测值,得到一个点的误差,在将所有数据点的误差累加,即可算出误差的和。但,这样做的可能存在正负值互相抵消的情况。因此,我们调整下公式并进行推导, 得到损失函数:

损失函数最小值
已经知道那么我们,我们现在的任务就是求出可以让损失函数达到最小值的点(α, β);注意到损失函数:

此外,我们还注意到α, β是两个未知变量,我们可以用通过先求偏导(注意链式法则的使用),并使其为0,再将所有实际值代入偏导数,最后求解方程组的方式计算出我们所需的α和β值。
计算损失函数偏导:
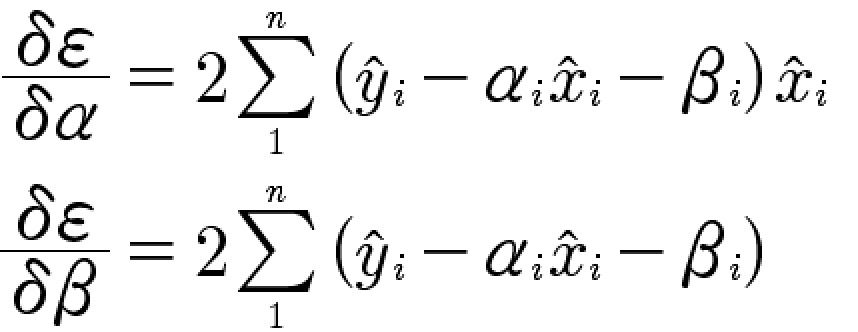
现在我们将训练集中的数据分别代入![]() 和
和![]() 计算损失函数偏导(注意,根据上文逻辑,训练集的每一组数据都能让对应的偏导数值为0),由于计算量比较大,我们通过gridstudio计算()。
计算损失函数偏导(注意,根据上文逻辑,训练集的每一组数据都能让对应的偏导数值为0),由于计算量比较大,我们通过gridstudio计算()。
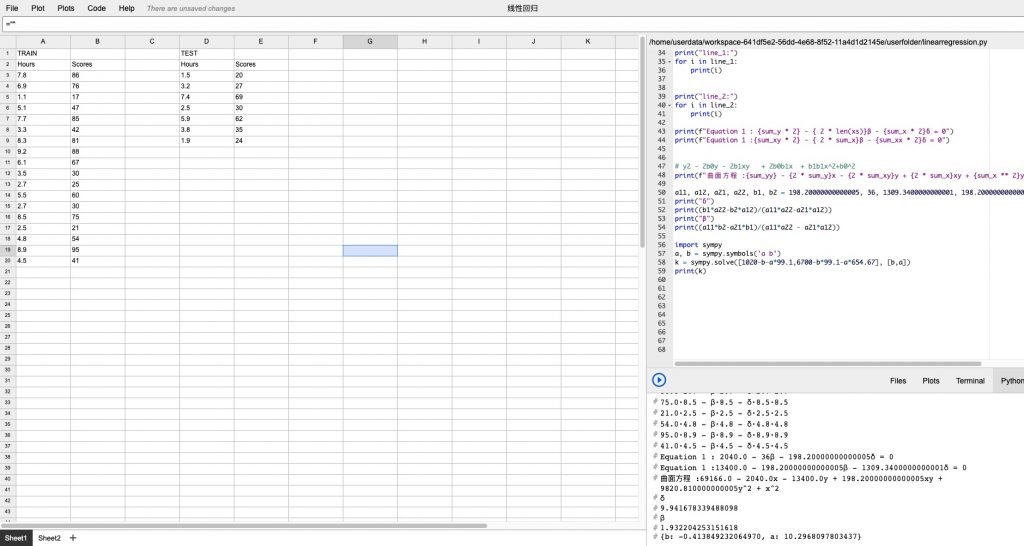
基本计算逻辑是将实际观测值代入偏导数,得到18(另α为0的方程组) + 18(另β为0的方程组)组方程,并将每个方程组的对应项累加。最终到两个方程(请自行忽略浮点数的问题):
最终解方程得到对应的α, β值:
α: -0.413849232064970;β: 10.2968097803437
到这一步,我们完成了代码 regressor = regressor.fit(X_train, Y_train) 背后的逻辑,也就真正学明白了“今天(day_2)”的内容。 给自己来杯咖啡奖励下自己吧。
gridstudio 及分析代码下载:
gridstudio:github
manual_linear_process.py 下载: Download
笔记下载
day_2.zip : Download


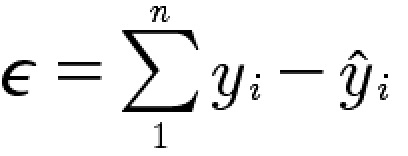
Comments NOTHING